Question

Without simplifying, select all the expressions that represent a rational number. Group of answer choices LaTeX: 4\frac{2}{3}+\frac{\sqrt{3}}{9} 4 2 3 + 3 9 4 2 3 + 3 9 4 2 3 + 3 9 LaTeX: 4\frac{2}{3}\times\frac{8}{\sqrt{3}} 4 2 3 × 8 3 4 2 3 × 8 3 4 2 3 × 8 3 LaTeX: 4\frac{2}{3}-\frac{\sqrt{4}}{8} 4 2 3 − 4 8 4 2 3 − 4 8 4 2 3 − 4 8 LaTeX: 4\frac{2}{3}\times\frac{\sqrt{3}}{9} 4 2 3 × 3 9 4 2 3 × 3 9 4 2 3 × 3 9 LaTeX: 4\frac{2}{3}\div\frac{\sqrt{4}}{8}

Answer 1

Option C.

Explanation:

We know the following properties,

1. Product of an irrational number and a non-zero rational number is always an irrational number.

2. Sum of a rational and an irrational number is always an irrational number.

3. Sum or products of rational numbers are always a rational number.

In option A,

`4(2)/(3)+(√(3))/(9)`

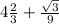
Here,
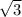`√(3)` is an irrational number.

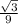`(√(3))/(9)` is an irrational number using property 1.

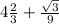`4(2)/(3)+(√(3))/(9)` is an irrational number using property 2.

So, using the above properties we can say that this expression represents an irrational number.

Similarly,

In option B,

`4(2)/(3)*(8)/(√(3))`

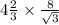
Here,
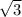`√(3)` is an irrational number. So, using the above properties we can say that this expression represents an irrational number.

In option C,

`4(2)/(3)-(√(4))/(8)`

Here,
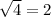`√(4)=2`, which is a rational number.

So, this expression represents a rational number using property 3.

In option D,

`4(2)/(3)*(√(3))/(9)`

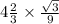
Here,
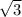`√(3)` is an irrational number. So, using the above properties we can say that this expression represents an irrational number.

Therefore, the correct option is C.