Question

Estimate the number of softballs that would fill a 10 by 12 by 24 foot room? Diameter of softball is 3.5 inches. Use the formula of a sphere V = 4/3 (3.14)r^3 for the softball

Answer 1

The number of softballs that would fill the room is 221796 softballs

Explanation:

First we will determine the Volume of the room.

The volume of a room is given by

`Volume = lwh`

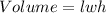
From the question, the given dimension of the room is 10 by 12 by 24 foot

Hence the volume of the room = 10 × 12 × 24

= 2880 cubic feet (ft³)

Convert to cubic inches

To do this, multiply the answer in cubic feet by (12 × 12 × 12)

(NOTE: 1 foot = 12 inches)

Hence, 2880 cubic feet = 2880 × 12 × 12 × 12 cubic inches

= 4976640 cubic inches

This is the volume of the room.

To estimate the number of softballs that would fill the room, we will determine the number of softballs which would give a total volume that is equal to the volume of the room.

First, we will find the volume of one softball

Diameter of softball = 3.5 inches

∴ Radius of softball, r = 3.5/2 inches = 1.75 inches

∴ r = 1.75 inches

Now, for the volume of one softball

From,

V = 4/3 (3.14)r^3

`V = (4)/(3)(3.14)r^(3)`

`V = (4)/(3)(3.14)` ×
`1.75^(3)`

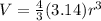
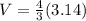`V = 22.43791667` cubic inches

This is the volume of one softball

The number of softballs that would fill the room will be

= Volume of the room / Volume of one softball

= 4976640 cubic inches / 22.43791667 cubic inches

=221795.9926

≅221796

Hence, the number of softballs that would fill the room is 221796 softballs