Question

20 POINTS: If tan= 3/4, find the CSC I don't know the relationship between tan and csc, please explain your answer

Answer 1

`\csc(x)=5/3`

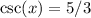
Explanation:

So we know that:

`\tan(x)=3/4`

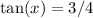
Recall that tangent represents the side opposite over the side adjacent.

This means that the opposite side is 3 while the adjacent side is 4.

Therefore, by using the Pythagorean Theorem, we can solve for the third side, which is the hypotenuse:

`a^2+b^2=c^2`

Substitute a for 3 and b for 4. Thus:

`3^2+4^2=c^2`

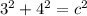
Square and add:

`9+16=c^2\\25=c^2`

Square root:

`c=5`

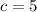
Now, recall that cosecant is the reciprocal of sine. So, find sine first.

Sine is opposite over hypotenuse. From tangent, the opposite is 3 and the hypotenuse as we now know is 5. Thus:

`\sin(x)=3/5`

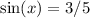
And cosecant is the reciprocal of that. Thus:

`\csc(x)=5/3`

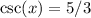
And that's our answer :)