Answer:
2 real roots
2 imaginary roots
Explanation:
So we have the function:

And we want to find its zeros.
First, let u equal x². So:
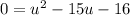
Factor:
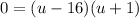
Zero Product Property:
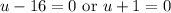
Add 16; Subtract 1. Replace u:
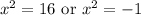
Take the square root:
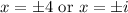
So, our solutions are 2 real roots and 2 imaginary roots.