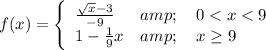Question

Hi guys, can anyone help me with this, Thanks a lot:)

Answer 1

`k=1/9`

Explanation:

A function is continuous at a point if and only if:

`\lim_(x \to n) f(x)=f(n)`

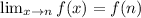
So, we have the piecewise function:

`f(x) = \left\{ \begin{array}{lI} (√(x) -3)/(-9) & \quad0< x <9 \\ 1-kx & \quad x\geq 9 \end{array} \right.$$`

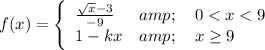
And we want to find the value of k such that the function is continuous.

First, find the left hand limit of f(x):

`\lim_(x\to9^-) f(x)`

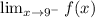
Since we're coming from the left, we'll use the first equation. Thus:

`=\lim_(x\to9^-) (√(x)-3)/(-9)`

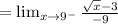
Direct substitution:

`=(√(9)-3)/(-9)`

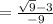
Simplify:

`=(3-3)/(-9)`

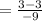
Subtract and divide:

`=(0)/(-9)=0`

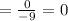
So, what this tells us is that for the function to be continuous, the right hand limit as f(x) approaches 9 from the right must also be equal to 0.

Therefore:

`\lim_(n \to 9^+) 1-kx=0`

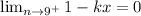
Direct substitution:

`1-9k=0`

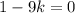
Subtract 1 from both sides:

`-9k=-1`

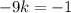
Divide both sides by -9:

`k=1/9`

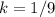
Therefore, the value of k is 1/9.

So, our equation in the end is:

`f(x) = \left\{ \begin{array}{lI} (√(x) -3)/(-9) & \quad0< x <9 \\ 1-(1)/(9)x & \quad x\geq 9 \end{array} \right.$$`

Answer 2

k = 1/9

Explanation:

In order for the function to be continuous at x=9, the values of the two expressions must be the same at x=9.

The first expression evaluates to ...

`(√(9)-3)/(-9)=-(3-3)/(9)=0`

The second expression needs to have the same value:

`1 -k(9) = 0\\\\1 = 9k\\\\\boxed{k=(1)/(9)}`