Question

The point-slope form of the equation that passes through (-4, -3) and (12, 1) is y - 1 = 1/4(x-12). what is the standard form of the equation for this line?

A) x-4y=8
B) x-4y=2
C) 4x-y=8
D) 4x-y=2

Answer 1

A

Explanation:

So we know that the point-slope form of the line that passes through the points (-4,-3) and (12,1) is:

`y-1=(1)/(4)(x-12)`

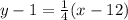
And we want to convert this to standard form.

The standard form of a linear equation is:

`Ax+By=C`

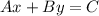
Where A, B, and C are integers, and, traditionally, A is positive.

So, first, multiply everything by 4 to remove the negative:

`4(y-1)=4((1)/(4)(x-12))`

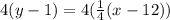
Distribute the left. The right cancels:

`4y-4=x-12`

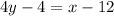
Add 4 to both sides. The left cancels:

`4y=x-8`

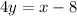
Subtract x from both sides:

`-x+4y=-8`

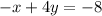
As I mentioned previously, the coefficient of A tends to be positive. So, divide everything by -1:

`(-x+4y)/-1=(-8)/-1`

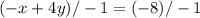
Simplify:

`x-4y=8`

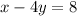
So, our answer is A

And we're done!