Answer:
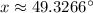
Explanation:
So we want to find Angle x.
Note that we already know the side length of the side opposite to Angle x.
We also know that the hypotenuse is 56.3.
Therefore, we can use the sine function. Recall that:
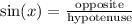
The opposite side is 42.7. The hypotenuse is 56.3. Substitute:
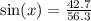
Take the inverse sine of both sides.
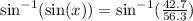
The left side cancels:
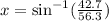
Use a calculator. Thus:
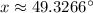
And that's our answer :)