Question

Please i need help When is the product of the square root of a prime number and a nonzero rational number a rational number?

Answer 1

The product of the square root of a prime number and a nonzero rational number is a irrational number.

Explanation:

Given that,

When is the product of the square root of a prime number and a nonzero rational number a irrational number.

We know that,

Prime number :

Prime number is that number whose has a two factor. first factor is one and second is themselves.

The square root of a prime number is irrational number.

Rational number :

Rational number is that number which is in fraction form.

For example :
`(p)/(q)`

Here, p and q are integers

We need to proof the product of the square root of a prime number and a nonzero rational number is a rational number

Using given data

Suppose, the square root = √5

Rational number =
`(2)/(3)`

We need to calculate the product of the square root of a prime number and a rational number

Using formula of product

`R=P*Q`

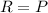
Where, P = square root of a prime number

Q= rational number

Put the value into the formula

`R=√(5)*(2)/(3)`

`R=(2√(5))/(3)`

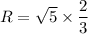
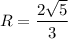
Hence, The product of the square root of a prime number and a nonzero rational number is a irrational number.