Answer:
First, we need to know how to calculate the area and the permiter of a rectangle.
To calculate the area, we multiply base by height and to calculate the perimeter, we sum all sides.
Knowing this, we can say that the area is 3x * (x+5) and the perimiter is 3x + 3x + x + 5 + x + 5, as we know both are the same, we write it as an equation:
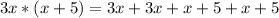
Now we solve the equation:
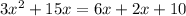
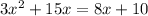
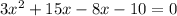
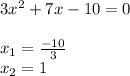
As the negative result doesn't have sense, we only pick the second one: 1.
If x = 1, then area would be 3*6 = 18 square inches and perimeter 3+3+6+6 = 18 inches