Question

A map of the town that Annie, Barbara, and Charlie live in can be represented by the Cartesian plane. Annie is located at $(6,-20)$ and Barbara is located at $(1, 14)$. They agree to meet at the closest point that is equidistant from their current locations and walk upwards together to get to Charlie's location at $\left(\frac{7}{2}, 2\right)$. How many units upward do Annie and Barbara walk together to get to Charlie?

Answer 1

5 units

Explanation:

Annie is located at (6,-20) and Barbara is located at (1, 14) and they meet at a point equidistant to their current locations.

This means that they have to meet at the midpoint between their two locations. Let the coordinate of the midpoint be (x,y) hence:

`x=(x_1+x_2)/(2)=(6+1)/(2) =(7)/(2)`

`y=(y_1+y_2)/(2)=(-20+14)/(2) =-3`

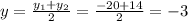
The point at which they met is at (7/2, -3). Charlie location is at (7/2, 2). Hence the distance upward that they have to move = 2 - (-3) = 5 units

They have to move 5 units upwards