Question

Multiplying two functions results in h(x) = 10x2 + 12x – 16, while adding the same functions results in j(x) = 7x. Which statements describe f(x) and g(x), the original functions? Select two options. Both functions must be linear. Both functions must be quadratic. Both functions must have a y-intercept of 0. The rate of change of either f(x) or g(x) must be 0. The y-intercepts of f(x) and g(x) must be opposites.

Answer 1

Both functions must be linear. The y-intercepts of f(x) and g(x) must be opposites.

Explanation:

First we need to solve.

h(x) = 10
`x^(2)` + 12
`x` - 16

It seems tricky at first but we know a couple things. When we add the factors of h(x) together we get j(x) = 7
`x` so we know that when we multiply 2 numbers together it should equal 10 but add up to 7.

Lets write the possible combinations of 10:

1 x 10 = 10

2 x 5 = 10

5 x 2 = 10

10 x 1 = 10

Now which combination will add or subtract to 7?

1 - 10 = 9 1 + 10 = 11

2 - 5 = -7 2 + 5 = 7 We can stop here!

2 and 5 are in our factor, so let's write it down.

(2x ) (5x ) We know there will one + and one - because the -16. If we had two + it would be positive 16, and is we had two - it would also be positive 16 because a - x - = +

Now the last number is 16. Let's find the possible combinations of 16.

1 x 16 = 16

2 x 8 = 16

4 x 4 = 16 We will stop here because we end up repeating posibilities.

Here is where we think critically. Whichever combination we choose has to be multiplied by 2 and 5 and end up equaling 12. I think 16 is too high so let's try 2 and 8.

2x * 2 = 4x 5x * 8 = 40x Now one is positive and the other is negative. Let's try each combination.

4x - 40x = -36x -4x + 40x = 36x Neither of those are 12x. So let's Try 4 and 4.

2x * 4 = 8x 5x * 4 = 20x One will be positive and the other will be negative. Let's try each combination.

8x - 20x = -12x -8x + 20x = 12x There is our combination! Remeber when you mutiply together you have to multiply the opposite factor. Here are the combinations:

(Ax + B )(Cx + D) = (Ax*Cx) + (Ax*D) + (B*Cx) + (B*D)

(Ax - B )(Cx + D) = (Ax*Cx) + (Ax*D) - (B*Cx) - (B*D)

(Ax + B )(Cx - D) = (Ax*Cx) - (Ax*D) + (B*Cx) - (B*D)

(Ax - B )(Cx - D) = (Ax*Cx) - (Ax*D) - (B*Cx) + (B*D)

So we have:

(2x + 4) (5x - 4)

Let's prove is and multiply it back out.

2x*5x - 2x*4 + 4*5x - 4*4

10
`x^(2)` - 8
`x` + 20

10
`x^(2)` + 12
`x` - 16 So we got it right!

Now let's see if they really add up to 7x.

(2x + 4) (5x - 4) which we now need to add together

2x + 4 + 5x - 4 Rearrange

2x + 5x + 4 - 4 Combine like terms

7x + 0 or 7x It works!

So our original functions are f(x) = 2x + 4 and g(x) = 5x - 4

Now to answer the question. Select 2 options.

Both functions must be linear. Yes, because an equation with only an
`x` will be a straight line, if we graph both functions they are both straight lines.

Both functions must be quadratic. No, because a quadratic equation is any equation that can be rearranged in standard form as
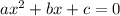`ax^(2) + bx +c = 0` Neither f(x) or g(x) can be rearranged to fit that.

Both functions must have a y-intercept of 0. No, to find the y intercept we set x to 0 and solve for y.

2x + 4 = y 5x - 4 = y

2(0) + 4 = y 5(0) - 4 = y

0 + 4 = y 0 - 4 = y

y = 4 y = -4

Neither are 0.

The rate of change of either f(x) or g(x) must be 0. Let's find the rate of change for each equation.

We need an interval so we have to find one. Let's use 1 and 2 for x, but we have to solve for y to get the coordinate.

f(x
`_(1)`) = 2x + 4 f(x
`_(2)`) = 2x + 4 g(x1) = 5x - 4 g(x2) = 5x - 4

x
`_(1)` = 1 x
`_(2)` = 2 x

y
`_(1)` = 2(1) + 4 y
`_(2)` = 2(2) + 4 y

y
`_(1)` = 2 + 4 y
`_(2)` = 4 + 4 y

y
`_(1)` = 6 y
`_(2)` = 8 y

( 1 , 6 ) ( 2 , 8 ) ( 1 , 1 ) ( 2 , 6 )

Rate of change formula is:

`(y_(2) - y_(1) )/(x_(2) - x_(1) )`

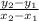
Now we just plug in for each function.

f(x) = 2x + 4 g(x) = 5x - 4

`(y_(2) - y_(1) )/(x_(2) - x_(1) )` =
`(8 - 6)/(2 - 1)` =
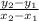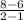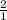`(2)/(1)` = 2

You can see the rate of change is not 0 for either function.

The y-intercepts of f(x) and g(x) must be opposites. Yes, we solved for the y intercepts earlier.

To find the y intercept we set x to 0 and solve for y.

2x + 4 = y 5x - 4 = y

2(0) + 4 = y 5(0) - 4 = y

0 + 4 = y 0 - 4 = y

y = 4 y = - 4

4 and - 4 are opposites, so this statement is also true.