Question

The base of a parallelogram is thrice its height. If the area is 897 sq.cm. Find the base and the height of parallelogram.

Answer 1

`\boxed{ \bold{ { \sf{height \: = \: 17.29 \: cm}}}}`

`\boxed{ \bold{ \sf{base = 51.87 \: cm}}}`

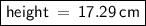
Explanation:

Let the height of a parallelogram be 'x'

Base of a parallelogram be 3x

Area of a parallelogram ( A ) = 897 cm²

Base ( b ) = ?

Height ( h ) = ?

First, finding the height of a parallelogram ( x )

`\bold{ \boxed{ \sf{area \: of \: a \: parallelogram \: = \: base \: * \: height}}}`

`\dashrightarrow{ \sf897 = 3x * x}`

`\dashrightarrow{ \sf{897 = 3 {x}^(2) }}`

`\dashrightarrow{ \sf{3 {x}^(2) = 897}}`

`\dashrightarrow { \sf{ \frac{3 {x}^(2) }{3} = (897)/(3) }}`

`\dashrightarrow{ \sf{ {x}^(2) = 299}}`

`\dashrightarrow{ \sf{x = √(299) }}`

`\dashrightarrow{ \sf{x = 17.29}}`

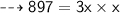
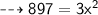
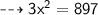
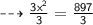
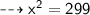
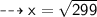
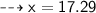
Height of a parallelogram = 17.29 cm

Finding the base of the parallelogram

`\sf{base \: of \ \: a \: parallelogram = 3x}`

⇒
`\sf{base \: of \: a \: parallelogram = \: 3 * 17.29}`

⇒
`\sf{base \: of \: a \: parallelogram = 51.87 \: cm}`

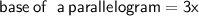
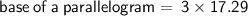
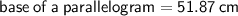
Base of a parallelogram = 51.87 cm

Hope I helped!

Best regards! :D