Question

How far is a chord of length 8 cm from the centre of a circle of radius 5 cm

Answer 1

3 cm

Explanation:

A line from the centre of the circle at right angles to the chord is a perpendicular bisector.

Thus a right triangle is formed with legs d , the line from centre to chord and 4 , half the length of the chord. The radius 5 is the hypotenuse.

Using Pythagoras' identity in the right triangle.

4² + d² = 5², that is

16 + d² = 25 ( subtract 16 from both sides )

d² = 9 ( take the square root of both sides )

d =
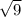`√(9)` = 3

Thus the chord is 3 cm from the centre of the circle.

Answer 2

• Answer:

OB = 3 cm

• Explanation:

AO = radius = 5 cm

AB = 8cm/2 = 4 cm

Pythagora

OB² = AO² - AB²

= (5cm)² - (4cm)²

= 25cm² - 16cm²

= 9 cm²

OB = √9cm²

= 3 cm