Answer:
as we know, the integral of
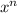 is
is
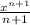
so, the integral of x.
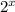 will be found as follows:
will be found as follows:
here, we will use a trick called 'integration by parts'
let x = u and
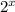 = v
= v
∫uv dx = u∫v dx - ∫[(du/dx)* ∫v dx] dx
∫x.
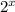 dx = x∫
dx = x∫
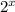 - ∫[(dx/dx) * ∫
- ∫[(dx/dx) * ∫
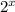 dx ] dx
dx ] dx
∫x.
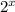 dx = x*
dx = x*
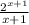 - 1 *
- 1 *
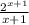
=
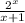 ( x - 1 )
( x - 1 )