Problem 4a
Let's say each figure has all side lengths that are 10 feet. You can pick any positve number you want.
For the regular octagon we have n = 8 and s = 10
Compute the area
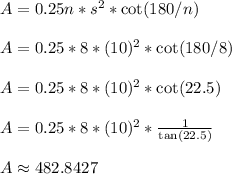
The regular octagon, with side lengths of 10 feet, has an area of roughly 482.8427 square feet.
-----------------
For the regular hexagon, we'll keep s = 10 but change n to n = 6
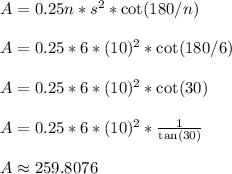
The regular hexagon (also with side length 10 ft) has an area of roughly 259.8076 square feet.
These numeric values aren't going to be part of the answer. All we care about which area is larger.
Comparing 482.8427 and 259.8076, we can see that the first value is larger, which corresponds to the octagon. Therefore, the octagon is larger.
-----------------
Answer:
The regular octagon has the greater area.
===========================================================
Problem 4b
Let's say both figures have an area of A = 100 square feet.
For the pentagon, we have n = 5 sides and we don't know the value of s.
Let's solve for it.
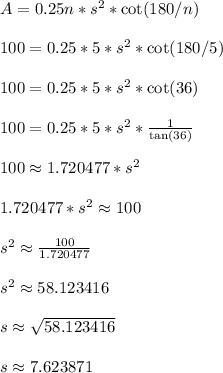
The side of the pentagon is about 7.62 feet to get us an area of 100 square feet.
Now let's follow the same type of steps for n = 6. Keep A = 100 the same.
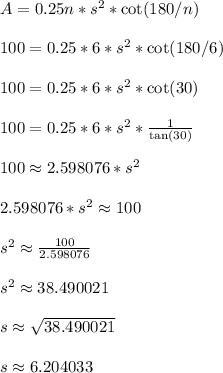
Each side length has become about 6.2 feet. The side length has gone down when n increased (if we kept the area the same).
The pentagon had a side length of 7.62 feet and the perimeter is about 5*7.62 = 38.1 feet.
Meanwhile, the hexagon has a side length of around 6.2 feet and perimeter of about 6*6.2 = 37.2 feet.
As n increases, the perimeter must decrease because each side must decrease. This is only if we wanted the area to stay the same.
-----------------
Answer:
The pentagon has the larger perimeter.