Answer:
23.26 years
Explanation:
Use the compound interest formula:
A = P
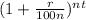
A = final amount
P = initial principal balance
r = interest rate
n = number of times interest applied per time period
t = number of time periods elapsed
P = $2,136.70
r = 2.7
n = 4
A = $4,000
Now we plug everything in and solve for t.
$4,000 = $2,136.70
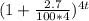
$4,000 = $2,136.70
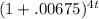
$4,000 = $2,136.70
 Divide each side by $2,136.70
Divide each side by $2,136.70
$4,000/$2,136.70 =

1.87 =

log (1.87) = log

log 1.87 = (4t) (log 1.00675) Divide each side by (log 1.00675)
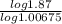 = 4t
= 4t
93.044 = 4t Divide each side by 4.
93.044/4 = t
23.26 = t
23.26 years