Question

NO LINKS!! Please help me with these​. Not a multiple choice

Answer 1

a) Parallelogram

b) 18 units

c) 12 + 2√13 units²

d) see attached and below

e) perimeter = 72 units

area = 24 + 4√13 units²

Explanation:

Given points:

• M = (-2, 1)
• A = (0, 4)
• T = (6, 4)
• H = (4, 1)

Part (a)

Shape of MATH: Parallelogram

Part (b)

`\begin{aligned}\textsf{Area of a parallelogram} & = \sf base * height\\& = (x_H-x_M) * (y_A-y_M)\\& = (4-(-2)) * (4-1)\\& = 6 * 3\\& = 18\: \sf units^2\end{aligned}`

Part (c)

`\begin{aligned}\textsf{Perimeter of MATH} & =2 * \sf base+2 * side\\& = 2 \textsf{MH} + 2 \textsf{AM}\\& = 2(4-(-2))+2(√(2^2+3^2))\\& = 2(6)+2(√(13))\\& = 12+2√(13)\: \sf units\end{aligned}`

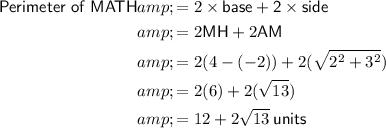
Part (d)

To dilate MATH with a dilation center at (0,0) and a dilation factor of 2, multiply the x and y coordinates of MATH by sf 2:

• M' = (-4, 2)
• A '= (0, 8)
• T' = (12, 8)
• H' = (8, 2)

Part (e)

As M'A'T'H' is an enlargement of MATH by a scale factor of 2, the perimeter of M'A'T'H' is twice that of MATH:

`\begin{aligned}\textsf{Perimeter of M'A'T'H'} & =2 * \textsf{perimeter of MATH}\\& = 2(12+2√(13))\\& = 24+4√(13)\: \sf units\end{aligned}`

As M'A'T'H' is an enlargement of MATH by a scale factor of 2, the area of M'A'T'H' is 2² that of MATH (as area is in 2 dimensions):

`\begin{aligned}\textsf{Area of M'A'T'H'} & =2^2 * \textsf{Area of MATH}\\& = 4(18)\\& = 72\: \sf units^2 \end{aligned}`