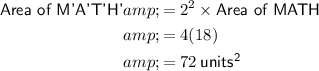Answer:
a) Parallelogram
b) 18 units
c) 12 + 2√13 units²
d) see attached and below
e) perimeter = 72 units
area = 24 + 4√13 units²
Explanation:
Given points:
- M = (-2, 1)
- A = (0, 4)
- T = (6, 4)
- H = (4, 1)
Part (a)
Shape of MATH: Parallelogram
Part (b)

Part (c)
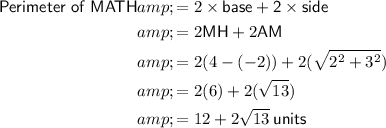
Part (d)
To dilate MATH with a dilation center at (0,0) and a dilation factor of 2, multiply the x and y coordinates of MATH by sf 2:
- M' = (-4, 2)
- A '= (0, 8)
- T' = (12, 8)
- H' = (8, 2)
Part (e)
As M'A'T'H' is an enlargement of MATH by a scale factor of 2, the perimeter of M'A'T'H' is twice that of MATH:
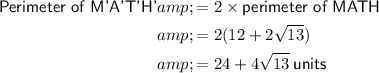
As M'A'T'H' is an enlargement of MATH by a scale factor of 2, the area of M'A'T'H' is 2² that of MATH (as area is in 2 dimensions):