Question

Which of the following circumstances would likely make factoring the best method for solving a quadratic equation?

Question 3 options:

A quadratic that is prime


The leading coefficient is zero


The leading coefficient is not 1 and the constant is a large number


The difference of 2 perfect squares

Answer 1

Option D.

Explanation:

We need to find the circumstances that would likely make factoring the best method for solving a quadratic equation.

A quadratic equation is prime if its factors can not possible. So, option A is incorrect.

In a quadratic equation leading coefficient can not be zero. So, option B is incorrect.

For large numbers (coefficient or constant), quadratic formula is best method. So, option C is incorrect.

The difference of 2 perfect squares is:

`x^2-a^2=(x-a)(x+a)`

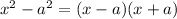
In this case factoring is the best method.

Therefore, the correct option is D.