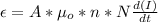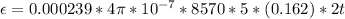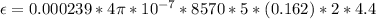Complete Question
A very long, straight solenoid with a cross-sectional area of 2.39cm2 is wound with 85.7 turns of wire per centimeter. Starting at t= 0, the current in the solenoid is increasing according to i(t)=( 0.162A/s2) t2. A secondary winding of 5 turns encircles the solenoid at its center, such that the secondary winding has the same cross-sectional area as the solenoid. What is the magnitude of the emf induced in the secondary winding at the instant that the current in the solenoid is 3.2A ?
Answer:
The value is

Step-by-step explanation:
From the question we are told that
The cross-sectional area is

The number of turns is
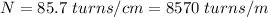
The initial time is t = 0s
The current on the solenoid is
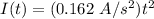
The number of turns of the secondary winding is

Generally At I = 3.2 A
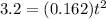
=>
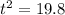
=>
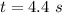
Generally induced emf is mathematically represented as