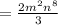Question

Select the correct answer Which is the correct simplified form of the expression (4m-2n^8)^1/2 ———— 9m^-6 n^-8

Answer 1

`= (2m^2n^8)/(3)`

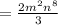
Explanation:

Given expression is

`((4m^(-2)n^8)/(9m^(-6)n^(-8)) )^{(1)/(2)`

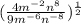
The correct simplified form is shown below:-

From the above equation, we will simplify

we will shift
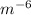`m^(-6)` to the numerator and we will use the negative exponent rule, that is

`= ((4m^(-2)n^8m^6)/(9n^(-8)) )^{(1)/(2)`

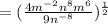
now we will shift the
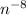`n^(-8)` to the numerator and we will use the negative exponent rule, that is

`= ((4m^(-2)n^8m^6n^8)/(9) )^{(1)/(2)`

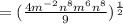
here we will solve the above equation which is shown below

`= ((4m^4n^(16))/(9)) ^(1)/(2)`

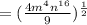
So,

`= (((2)^2(m^2)^2(n^8)^2)/((3)^2) ^(1)/(2)`

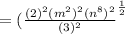
Which gives result

`= (2m^2n^8)/(3)`