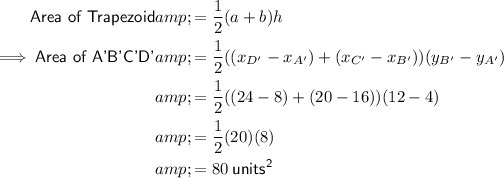Answer:
Given points
- A = (2, 1)
- B = (4, 3)
- C = (5, 3)
- D = (6, 1)
Part (a)
See attached
Part (b)
Trapezoid
Part (c)
To dilate ABCD with a dilation center at (0,0) and a dilation factor of 4, multiply the x and y coordinates of ABCD by sf 4:
- A' = (8, 4)
- B' = (16, 12)
- C' = (20, 12)
- D' = (24, 4)
Part (d)