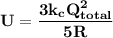Answer:
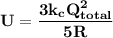
Step-by-step explanation:
From the information given;
The surface area of a sphere =
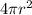
If the sphere is from the collection of spherical shells of infinitesimal thickness = dr
Then,
the volume of the thickness and the sphere is;
V =
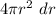
Using Gauss Law
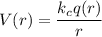
here,
q(r) =charge built up contained in radius r
since we are talking about collections of spherical shells, to work required for the next spherical shell r +dr is
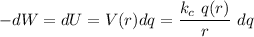
where;
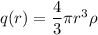
dq which is the charge contained in the next shell of charge
here dq = volume of the shell multiply by the density
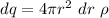
equating it all together
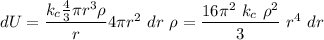
Integration the work required from the initial radius r to the final radius R, we get;
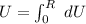
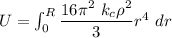
![U = \int^R_0 (16 \pi^2 \ k_c \rho^2)/(3) [(r^5)/(5)]^R_0](https://img.qammunity.org/2021/formulas/physics/college/lccp53q11a281ybptjlz2h6l6thqdd2a6v.png)
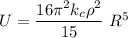
Recall that:
the total charge on a sphere, i.e
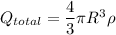
Then :