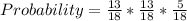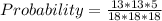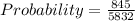Question

roll two standard dice and add the numbers. what is the probability of getting a number larger than 8 for the first time on the third roll

Answer 1

`Probability = (845)/(5832)`

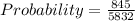
Explanation:

Given

Two standard dice

Required

Probability that the outcome will be greater than 8 for the first time on the third roll

First, we need to list out the sample space of both dice

`S_1 = \{1,2,3,4,5,6\}`

`S_2 = \{1,2,3,4,5,6\}`

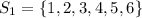
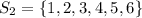
Next, is to list out the sample when outcome of both dice are added together
`S = \{2,3,4,5,6,7,3,4,5,6,7,8,4,5,6,7,8,9,5,6,7,8,9,10,6,7,8,9,10,11,7,8,9,10,11,12\}`

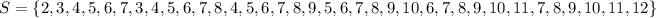
Next, is to get the probability that an outcome will be greater than 8

Represent this with P(E)

`P(E) = (Number\ of\ outcomes\ greater\ than\ 8)/(Total)`

`P(E) = (10)/(36)`

`P(E) = (5)/(18)`

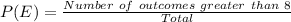
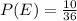
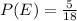
Next, is to get the probability that an outcome will noy be greater than 8

Represent this with P(E')

`P(E) + P(E') = 1`

`P(E') = 1 - P(E)`

`P(E') = 1 - (5)/(18)`

`P(E') = (18 - 5)/(18)`

`P(E') = (13)/(18)`

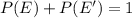
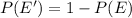
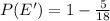
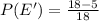
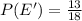
Now, we can calculate the required probability;

Probability of a number greater than 8 first on the third attempt is:

Probability of outcome not greater than 8 on the first attempt * Probability of outcome not greater than 8 on the second attempt * Probability of outcome greater than 8 on the third attempt

Mathematically;

`Probability = P(E') * P(E') * P(E)`

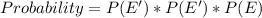
Substitute values for P(E) and P(E')

`Probability = (13)/(18) * (13)/(18) * (5)/(18)`

`Probability = (13 * 13 * 5)/(18 * 18 * 18)`

`Probability = (845)/(5832)`