Question

Find the nth Taylor polynomial for the function, centered at c. f(x) = ln(x), n = 4, c = 3 P4(x) =

Answer 1

P₄(x) = ln3 + 1/3 (x-3) - 1/9*2! (x-3)² + 2/27*3! (x-3)³ - 2/27*4! (x - 3)⁴

Explanation:

Given:

f(x) = ln(x)

n = 4

c = 3

To find:

nth Taylor polynomial for the function, centered at c

Solution:

The Taylor series for f(x) = ln x centered at 3 is:

`P_(n)(x) = f(c) + (f'(c))/(1!)(x-c)+(f''(c))/(2!)(x-c)^(2) +(f'''(c))/(3!)(x-c)^(3)+...+(f^(n) (c))/(n!)(x-c)^(n)`

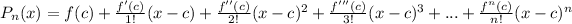
Since c = 3 So,

`P_(4)(x) = f(3) + (f'(3))/(1!)(x-3)+(f''(3))/(2!)(x-3)^(2) +(f'''(3))/(3!)(x-3)^(3)+...+(f^(n) (3))/(n!)(x-3)^(n)`

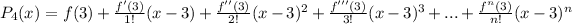
Now

f(3) = ln 3

f'(x) = 1/x ⇒ f'(3) = 1/3

f''(x) = -1/x² ⇒ f''(3) = -1/3² = -1/9

f'''(x) = 2/x³ ⇒ f'''(3) = 2/3³ = 2/27

f
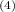`^((4))` (x) = -6/x⁴ ⇒ f
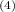`^((4))` (3) = -6/3⁴ = -6/81 = - 2/27

So Taylor polynomial for n=4 is:

P₄(x) = ln3 + 1/3 (x-3) - 1/9*2! (x-3)² + 2/27*3! (x-3)³ - 2/27*4! (x - 3)⁴