Question

Find the volume of the solid generated when R​ (shaded region) is revolved about the given line. x=6−3sec y​, x=6​, y= π 3​, and y=​0; about x= 6

Answer 1

`V=9\pi√(3)`

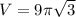
Explanation:

In order to solve this problem we must start by graphing the given function and finding the differential area we will use to set our integral up. (See attached picture).

The formula we will use for this problem is the following:

`V=\int\limits^b_a {\pi r^(2)} \, dy`

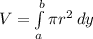
where:

`r=6-(6-3 sec(y))`

`r=3 sec(y)`

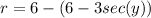
a=0

`b=(\pi)/(3)`

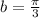
so the volume becomes:

`V=\int\limits^(\pi)/(3)_0 {\pi (3 sec(y))^(2)} \, dy`

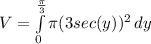
This can be simplified to:

`V=\int\limits^(\pi)/(3)_0 {9\pi sec^(2)(y)} \, dy`

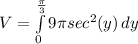
and the integral can be rewritten like this:

`V=9\pi\int\limits^(\pi)/(3)_0 {sec^(2)(y)} \, dy`

which is a standard integral so we solve it to:

`V=9\pi[tan y]\limits^(\pi)/(3)_0`

so we get:

`V=9\pi[tan (\pi)/(3) - tan 0]`

which yields:

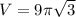`V=9\pi√(3)`]