Answer:
278.482 kilograms of water must be evaporated each hour.
Explanation:
Initial mass of cereal is equal to the product of cereal mass-to-mass ratio and total mass flow:
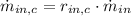
Where:
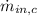 - Inlet cereal mass flow, measured in kilograms per hour.
- Inlet cereal mass flow, measured in kilograms per hour.
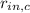 - Inlet cereal mass ration, dimensionless.
- Inlet cereal mass ration, dimensionless.
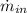 - Cereal product mass flow, measured in kilograms per hour.
- Cereal product mass flow, measured in kilograms per hour.
If
 and
and
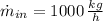 , then:
, then:
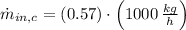
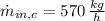
The initial mass flow of water is:
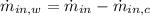

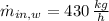
Given that final total mass flow contains only 21 % water, the final water mass flow, measured in kilograms per hour, is:
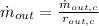
(
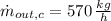 ,
,
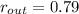 )
)
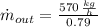
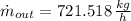
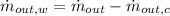
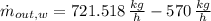
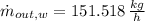
Finally, the amount of water that must be evaporated per hour is:
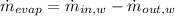
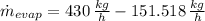
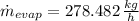
278.482 kilograms of water must be evaporated each hour.