Step-by-step explanation:
The resistance of a wire is given by the formula as follows :
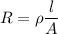
l is length of wire
A is area of cross section,
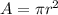
Since, r=d/2, d = diameter
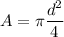
It is given in the problem that the resistance of two aluminum wires is same.
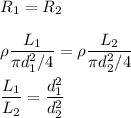
We have, L₁=2L₂
So,
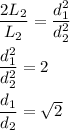
So, the ratio of the diameter of the longer wire to the diameter of the shorter wire is
