Question

I need help with these two trigonometry problems.

Find each measurement indicated. Round your answers to the nearest tenth.

Answer 1

Explanation:

For 5 we need to use sine law.

The thing about sine law is that we need to look at the triangle sides that are in front of the angles.

In this case: <B = 30°

the triangle side that is in front of this angle is AC which is 4 cm.

Then we got <C = 61°, and the triangle side in front of it is AB, which is what we need to find.

According to sine law:

`(sin B)/(AC) = (sin C)/(AB)`

`(sin 30)/(4) = (sin 61)/(AB)`

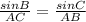
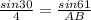
Notice that you need to be consistent. If you start writing that the angle is in the numerator, it needs to be in the numerator on the other side of the equation.

Solving it would give us:

(AB )(sin 30) = (sin 61)(4)

AB = 6.9969 cm

to the nearest tenth it's 7.0 cm

Question 6:

Wow it's pretty crowded, but they probably want us to use sine law as well. Let's write what we know:

<C = 12°

<B = 107°

AB = 21 yd

AC = ?

Apply it to the formula: sin(angle) / the triangle side in front of it.

`(sin 12)/(21) = (sin 107)/(AC)\\`

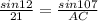
(sin 107)(21) = (sin 12)(AC)

AC = 96.59

to the nearest tenth AC = 96.6 yd