Explanation:
Hey, there!!
Here, the given point is (1,3).
Now, Using one point formula we need to find the equation of the line passing through point (1,3).
Now,
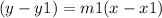
Keeping values,
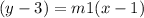
It is the 1st equation.
Similary, you have another equation,
2y = 4x + 8..............2nd equation.
or, 4x - 2y +8 =0
M2 from equation 2,
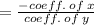
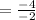
Therefore, m2 = 2
Now,
As per the condition of parallel lines,
m1 = m2 = 2
Now, substituting the value of m1 in equation 1st.
(y-3) = 2 (x-1)
y-3 = 2x - 2
or, 2x-y+1 = 0 ......is the required equation.
Hope it helps...