Answer:
9 °C
Explanation:
Given function:
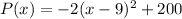
The given function is a quadratic in vertex form.
Vertex form:
 (where (h, k) is the vertex)
(where (h, k) is the vertex)
Therefore, the vertex is (9, 200)
The vertex is the minimum point for a parabola that opens upward.
The vertex is the maximum point for a parabola that opens downward.
The given function has a negative leading coefficient, therefore is opens downwards, and the vertex is the maximum point.
Therefore, the temperature (x-value) that will give the maximum number of fish (y-value) is the x-value of the vertex: 9 °C