Answer:
C - with explanation
Explanation:
First, when you graph an inequality that uses a < or > it's plotted with a dashed line to show the line isn't included in the region.
Inequalities with a
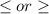 are plotted with a solid line to show the line is included in the region.
are plotted with a solid line to show the line is included in the region.
You can eliminate B and D because they are showing a graph using < or >
Now we know it's either A or C.
To figure out each, let's pick 4 random points, one in each quadrant and color.
Let's pick (3,3) (3, -3) (-3,3) (-3,-3) For an easier visual they would be
|
(-3,3) | (3,3)
___________|____________
|
(-3,-3) | (3,-3)
|
Plus in the values for each inequality:
(3,3) x + 2y
 4 3x - y
4 3x - y
 2
2
3 +
 2(3) 3(3) - 3
2(3) 3(3) - 3
3 + 6 = 9 9 - 3 = 6
9 is not
 to 4 6 is
to 4 6 is
 2
2
So this is a valid point because it works in the 2nd equation.
We got lucky and the first point we chose eliminates option A because (3,3) is a point that works and option A shows that area as being "out of bounds."
To test option C let's pick a point in the undefined area. Let's choose (-1,3)
(-1,3) x + 2y
 4 3x - y
4 3x - y
 2
2
-1 +
 2(3) 3(-1) - 3
2(3) 3(-1) - 3
-1 + 6 = 5 -3 - 3 = - 6
5 is not
 to 4 -6 is not
to 4 -6 is not
 2
2
So this point in the white area is not valid for either inequality.
Now we know for sure the correct option is C.