Question

Probe that:

`\sec \alpha \sqrt{1 - \sin( {}^(2) ) } \alpha = 1`
​

Answer 1

Explanation:

`\sec \alpha \sqrt{1 - \sin ^(2) \alpha } = 1`

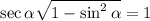
Prove the LHS

Using trigonometric identities

That's

`\cos ^(2) \alpha = 1 - \sin^(2) \alpha`

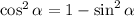
Rewrite the expression

We have

`\sec \alpha \sqrt{ \cos^(2) \alpha }`

`\sqrt{ { \cos }^(2) \alpha } = \cos \alpha`

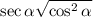
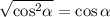
So we have

`\sec \alpha * \cos \alpha`

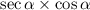
Using trigonometric identities

`\sec \alpha = (1)/( \cos \alpha )`

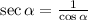
Rewrite the expression

That's

`(1)/(\cos \alpha ) * \cos \alpha`

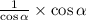
Reduce the expression with cos a

We have the final answer as

1

As proven

Hope this helps you