Question

Find the 7th term in the
sequence
-1, -3, -9,...

Answer 1

The answer is 729

Step-by-step explanation:

to get the next term, the sequence multiples the previous number by -3

1 * -3 = -3

-3 * -3 = 9

and so on.

To get the 7th term:

-27 * -3 = 81 (5th term)

81 * -3 = -243 (6th)

-243 * -3 = 729 (7th)

Answer 2

The seventh term in the sequence is -729.

Explanation:

Notice that the sequence is not increasing linearly. Therefore, this is a geometric sequence.

Recall that the explicit formula for a geometric sequence is given by:

`x_n=a(r)^(n-1)`

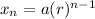
Where a is the first term, r is the common ratio, and n denotes the nth term.

From the sequence, we can see that our first term a is -1.

Because each term is thrice the previous, our common ratio r is 3.

By substitution:

`x_n=-(3)^(n-1)`

Hence, the seventh term is:

`\displaystyle \begin{aligned} x_7 & = -(3)^((7)-1) \\ \\ & = -(3)^(6) \\ \\ & = -729\end{aligned}`

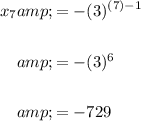
In conclusion, the seventh term is -729.