Question

Factoring the expression 20a^3b^3 – 24a^5b^2 + 4a^3b^2 gives a new expression of the form

Ua^xb^y (Wa^2 + Vb+ z), where U > 0.
What is the value of U?
What is the value of W?
What is the value of V?
What is the value of Z?
What is the value of x?
What is the value of y?

Answer 1

`U = 4\\W = -6\\V = 5\\Z = 1\\x = 3\\y = 2`

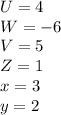
Explanation:

Then given expression is:

`20a^3b^3-24a^5b^2+4a^3b^2`

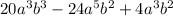
To express the given expression in the form:

`Ua^xb^y(Wa^2+Vb+Z)`

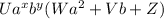
and to find the values of
`U, W, V, Z, x, y`.

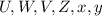First of all, let us check the maximum common powers of
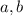`a, b` in each term from the given expression.

The maximum common power of
`a` is 3 and

The maximum common power of
`b` is 2.

So, we can take
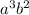`a^3b^2` common out of each term.

And maximum common coefficient that can be taken out common is 4.

Taking 4
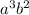`a^3b^2` common from each term of given expression, we get:

`4a^3b^2(-6a^2+5b+1)`

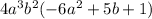
Now, let us compare the given term with:

`4a^3b^2(-6a^2+5b+1)` =
`Ua^xb^y(Wa^2+Vb+Z)`

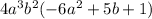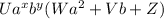
Now, the values that we get the following values:

`U = 4\\W = -6\\V = 5\\Z = 1\\x = 3\\y = 2`

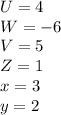
which is our answer.