Answer:
592 hours
Explanation:
Given
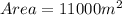
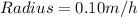
Required
Determine the time taken to cover the area
Since, the oil formed a circular pattern; the question will be answered using area of a circle
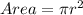
Let t represent the time take to cover 11000m²;
The relationship between these parameters is:
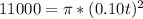
Substitute 3.14 for π
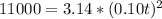
Divide both sides by 3.14
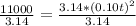
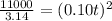
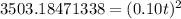
Take square root of both sides
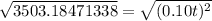
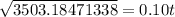
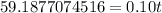
Divide both sides by 0.10
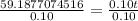
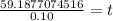
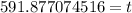
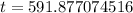
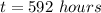 (Approximated)
(Approximated)
Hence, it'll take approximately 592 hours to cover the given area