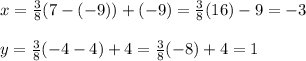Question

Given directed line segment QS , find the coordinates of R

such that the ratio of QR to RS is 3:5. Plot point R

Answer 1

Answer: It’s 2.6

Explanation:

Answer 2

The answer is below

Explanation:

The question is not complete, what are the coordinates of point Q and R. But I would show how to solve this.

The location of a point O(x, y) which divides line segment AB in the ratio a:b with point A at (
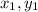`x_1,y_1`) and B(
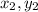`x_2,y_2`) is given by the formula:

`x=(a)/(a+b)(x_2-x_1)+x_1\\ \\y=(a)/(a+b)(y_2-y_1)+y_1`

If point Q is at (
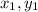`x_1,y_1`) and S at (
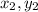`x_2,y_2`) and R(x, y) divides QS in the ratio QR to RS is 3:5, The coordinates of R is:

`x=(3)/(3+5)(x_2-x_1)+x_1=(3)/(8)(x_2-x_1)+x_1\\ \\y=(3)/(3+5)(y_2-y_1)+y_1=(3)/(8)(y_2-y_1)+y_1`

Let us assume Q(−9,4) and S(7,−4)

`x=(3)/(8)(7-(-9))+(-9)=(3)/(8)(16)-9=-3\\\\y=(3)/(8)(-4-4)+4=(3)/(8)(-8)+4=1`