Question

If f(x)=ln x then limx→2 f(x)= 1 2 Infinite Does Not Exist None of the above

Answer 1

`\lim_(x \to 2^(+)) f(x) = 2`

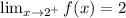
None of the above.

Explanation:

f(x) = [x], in the graphing calculator, is f(x) = int(x).

This means we take the floor of x, or round down all the time.

The question is asking us to find the limit as x approaches 2 from the right. Since the graph from [2, 3) is going to be y = 2, we know that if we are approaching from the right of x → 2, we will approach y = 2 (shown in graph).

If we were to approach x → 2 from the left, then we would approach y = 1 (shown in graph).

If we were to approach from both the left and the right, then we would get DNE.