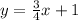Question

Write the slope-intercept form of the line passing through (–8, –5) and (4, 4).

Answer 1

`\Huge \boxed{y=(3)/(4) x+1}`

`\rule[225]{225}{2}`

Explanation:

We can find the slope through two points.

m = (y2 - y1)/(x2 - x1)

m = (4 - -5)/(4 - -8)

m = 9/12 = 3/4

The slope of the line is 3/4.

Slope-intercept form of a line is y=mx+b. Where m is the slope and b is the y-intercept.

y = 3/4x + b

A point on the line is (4, 4). x = 4 and y =4.

4 = 3/4(4) + b

4 = 3 + b

b = 1

The y-intercept is 1.

`\rule[225]{225}{2}`

Answer 2

`\huge\boxed{y = (3)/(4)x+1}`

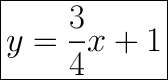
Explanation:

Finding the slope (m) first:

Given the coordinates (-8 , -5) and ( 4 , 4 )

Slope =
`\sf (Rise)/(Run)`

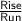
Slope =
`\sf (y2-y1)/(x2-x1)`

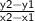
Slope =
`(4 + 8)/(4+5)`

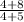
Slope =
`(12)/(9)`

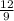
Slope = m =
`(3)/(4)`

Finding y - intercept (b) :

Taking a coordinate say (4,4)

And putting it in slope intercept form along with b

y = mx+b

Where y = 4 , m = 3/4 and x = 4

4 = (3/4)(4) + b

4 = 3+b

4-3 = b

1 = b

So,

b = 1

Putting m and b now in slope-intercept equation:

y = mx+b

`y = (3)/(4)x+1`