Answer:
 .
.
Step-by-step explanation:
Fact: The weight of the box on the said planet would be
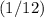 the weight on the earth:
the weight on the earth:
Let
 and
and
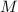 denote the radius and mass of planet earth, respectively. Let
denote the radius and mass of planet earth, respectively. Let
 denote the mass of the box. Let
denote the mass of the box. Let
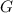 denote the gravitational constant.
denote the gravitational constant.
If the earth is a uniform sphere, the weight of this box on earth would be:
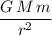 .
.
On a spherical planet with mass
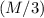 and radius
and radius
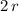 , the weight of this box on that planet would be:
, the weight of this box on that planet would be:
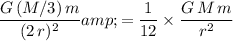 .
.
In other words, the weight of this box on the said planet would be
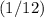 of the weight of this box on the earth.
of the weight of this box on the earth.
The board exerts (kinetic) friction on the box while the box slides across this board. The magnitude of this friction force is proportional to the magnitude of the normal force that the board exerts on the box.
Since this board is horizontal, the magnitude of this normal force would be equal to the weight of the box. Thus, the magnitude of the friction in this question would be proportional to the the weight of this box.
When the weight of this box is reduced (in magnitude) to
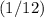 of the value on the earth, the magnitude of this friction would also be reduced to
of the value on the earth, the magnitude of this friction would also be reduced to
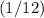 of the original value. Thus, the magnitude of the friction on the said planet would be
of the original value. Thus, the magnitude of the friction on the said planet would be
 .
.