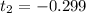Answer:
The points are
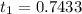
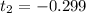
Explanation:
From the question we are told that
The first equation is
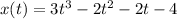
The second equation is
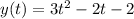
Now differentiating the first and second equation
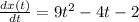
and
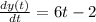
Now
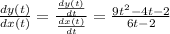
at critical point
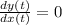
=> \frac{9t^2 -4t-2}{6t-2}=0[/tex]
=>

solving using quadratic formula we have that
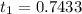
and