Question

Effciency of a lever is never 100% or more. why?Give reason​

Answer 1

Ideally, the work output of a lever should match the work input. However, because of resistance, the output power is nearly always be less than the input power. As a result, the efficiency would go below
`100\%`.

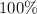Step-by-step explanation:

In an ideal lever, the size of the input and output are inversely proportional to the distances between these two forces and the fulcrum. Let
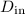`D_\text{in}` and
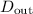`D_\text{out}` denote these two distances, and let
`F_\text{in}` and
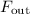`F_\text{out}` denote the input and the output forces. If the lever is indeed idea, then:

`F_\text{in} \cdot D_\text{in} = F_\text{out} \cdot D_\text{out}`.

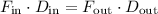Rearrange to obtain:

`\displaystyle F_\text{in} = F_\text{out} \cdot \frac{D_\text{out}}{D_\text{in}}`

Class two levers are levers where the perpendicular distance between the fulcrum and the input is greater than that between the fulcrum and the output. For this ideal lever, that means
`D_\text{in} > D_\text{out}`, such that
`F_\text{in} < F_\text{out}`.

Despite
`F_\text{in} < F_\text{out}`, the amount of work required will stay the same. Let
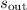`s_\text{out}` denote the required linear displacement for the output force. At a distance of
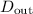`D_\text{out}` from the fulcrum, the angular displacement of the output force would be
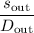`\displaystyle \frac{s_\text{out}}{D_\text{out}}`. Let
`s_\text{in}` denote the corresponding linear displacement required for the input force. Similarly, the angular displacement of the input force would be
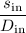`\displaystyle \frac{s_\text{in}}{D_\text{in}}`. Because both the input and the output are on the same lever, their angular displacement should be the same:

`\displaystyle \frac{s_\text{in}}{D_\text{in}} =\frac{s_\text{out}}{D_\text{out}}`.

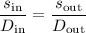Rearrange to obtain:

`\displaystyle s_\text{in}=s_\text{out} \cdot \frac{D_\text{in}}{D_\text{out}}`.

While increasing
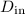`D_\text{in}` reduce the size of the input force
`F_\text{in}`, doing so would also increase the linear distance of the input force
`s_\text{in}`. In other words,
`F_\text{in}` will have to move across a longer linear distance in order to move
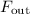`F_\text{out}` by the same
`s_\text{out}`.

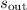The amount of work required depends on both the size of the force and the distance traveled. Let
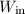`W_\text{in}` and
`W_\text{out}` denote the input and output work. For this ideal lever:

`\begin{aligned}W_\text{in} &= F_\text{in} \cdot s_\text{in} \\ &= \left(F_\text{out} \cdot \frac{D_\text{out}}{D_\text{in}}\right) \cdot \left(s_\text{out} \cdot \frac{D_\text{in}}{D_\text{out}}\right) \\ &= F_\text{out} \cdot s_\text{out} = W_\text{out}\end{aligned}`.

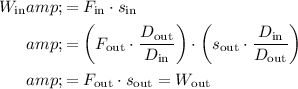In other words, the work input of the ideal lever is equal to the work output.

The efficiency of a machine can be measured as the percentage of work input that is converted to useful output. For this ideal lever, that ratio would be
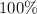`100\%`- not anything higher than that.

On the other hand, non-ideal levers take in more work than they give out. The reason is that because of resistance,
`F_\text{in}` would be larger than ideal:

`\displaystyle F_\text{in} = F_\text{out} \cdot \frac{D_\text{out}}{D_\text{in}} + F(\text{resistance})`.

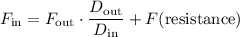As a result, in real (i.e., non-ideal) levers, the work input will exceed the useful work output. The efficiency will go below
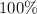`100\%`,