Question

Thanks for the help!

Answer 1

A

Explanation:

So we have the piecewise function:

`f(x)= \begin{cases}√(2x) & \text{if }x<3 \\2x+10 & \text{if }3\leq x<8\\42&\text{if } x\geq 8\end{cases}`

And we want to find f(8).

Since our input value is 8, choose the equation that fits our input.

The first equation demand x to be less than 3. 8 is not less than 3, so we won't use that.

The second equation demand x to e greater than or equal to 3 and less than 8. 8 is not less than 8. So, we won't use that.

The third equation demands x to be greater than or equal to 8. 8 is greater than or equal to 8, so we'll use the third equation.

So:

`f(x)=42\text{ if }x\geq 8`

`f(8)=42`

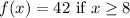
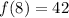
There're nothing more to do, we're done :)

The answer is A.

Edit: Improved Format