Question

PLEASE GUYS, I NEED HELP

Q1. What is the simplified form of 5(x-3y)+4(4y-x)-2(x-y)?


Q2. What is the solution set of 3-2[x+2]=6?


Q3. Which of the following is true about the row data given below 4, 7, 8, 4 and 1?

A. The median is 6
B. The mean is equal to the median
C. The mode is equal to the median
D. The range is 8

Q4. Which of the following is the slope of the line passing through the points A(1-a,b+1) and B(1+a,1-b)?


`a. \: (1 - b)/(1 + a) \\ \\ b. \: \: (b + 2)/(a - 2) \\ \\ c. \: \: \: (b)/(a) \\ \\ d. \: ( - b)/(a )`



​

Answer 1

d

Explanation:

Answer 2

see explanation

Explanation:

(1)

5(x - 3y) + 4(4y - x) - 2(x - y) ← distribute all 3 parenthesis

= 5x - 15y + 16y - 4x - 2x + 2y ← collect like terms

= 3y - x

(2)

3 - 2(x + 2) = 6 ( subtract 3 from both sides )

- 2(x + 2) = 3 ( divide both sides by - 2 )

x + 2 = - 1.5 ( subtract 2 from both sides )

x = - 3.5

solution set = { - 3.5 }

(3)

The median is the middle value of the data in ascending order

1 4 4 7 8 ← in ascending order

↑ median = 4

The mean is the sum of the values divided by the count

mean =
`(1+4+4+7+8)/(5)` =
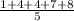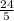`(24)/(5)` = 4.8

The mode is the value which occurs most often

mode = 4

Thus the mode is equal to the median → C

(4)

Calculate the slope m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

with (x₁, y₁ ) = (A(1 - a, b + 1 ) and (x₂, y₂ ) = B(1 + a, 1 - b )

m =
`(1-b-(b+1))/(1+a-(1-a))`

=
`(1-b-b-1)/(1+a-1+a)`

=
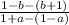
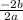`(-2b)/(2a)` ( cancel 2 on numerator/ denominator )

=
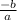`(-b)/(a)` → d