Answer : The incorrect step is, (A) step 1: -10 + 6x > 8
Step-by-step explanation :
The given expression is:
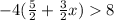
Now solving this expression step by step.
First -4 distributed over parentheses.
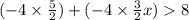
Now solving bracket term, we get:
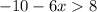
Now taking like terms together, we get:
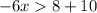
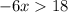
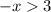
Now multiplying this expression by (-1), we get:
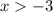
Thus, the incorrect step is, (A) step 1: -10 + 6x > 8