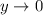Question

Give the largest interval over which the general solution is defined. (Think about the implications of any singular points. Enter your answer using interval notation.) Determine whether there are any transient terms in the general solution. (Enter the transient terms as a comma-separated list; if there are none, enter NONE.)

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

No singular point due to the exponent in the solution

The interval is
`-\infty  <0 <  \infty`

b

NONE

Explanation:

From the question we are told that

`(dy)/(dx) =  9y`

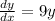
The generally solution is mathematically represented as

`(dy )/(dx)  =  9y`

=>
`(dy)/(y)  =  9dx`

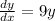
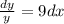
integrating both sides

`\int\limits  {( dy)/(y) } \,  = \int\limits  {9} \, dx`

=>
`lny = 9x + c`

=>
`y =  e^(9x +c )`

=>
`y =  e^(9x) e^(c)`

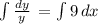
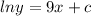
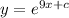
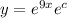
Here
`e^c  =  C`

=>
`y = C  e^(9x)`

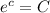
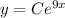
From the above equation we see that the domain for x has no singular point the interval is

`-\infty  <0 <  \infty`

Also there is no transient term in the general solution obtained because as
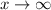`x \to \infty` there no case where
`y \to 0`