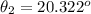Answer:
The value is
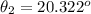
Step-by-step explanation:
From the question we are told that
The angle of the first order maximum is
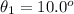
Generally the condition for constructive interference is

Here d is the separation between the slit ,
n is the order of maxima with values n = 1, 2 , 3 ... for first , second , third ... order of maxima
Now for first order of maximum
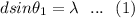
=>
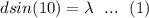
Now for second order of maximum
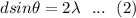
dividing equation 1 by 2
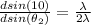
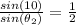
=>
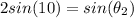
=>
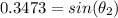
=>
![\theta_2 = sin^(-1) [0.3473]](https://img.qammunity.org/2021/formulas/physics/college/fb2mbq0cai39lw8mhgv435ff4ri8w7lmy0.png)
=>