Question

Pls help It’s due tomorrow question is in the picture

Answer 1

C

Explanation:

Let's find the area of each of the two circles.

First Circle:

The first circle has a diameter of 10 inches. That means the radius is 5 inches. So, its area is:

`A=\pi r^2\\A=\pi (5)^2\\A=25\pi`

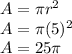
Second Circle:

The second circle has a diameter twice that of the first. So, the diameter is 20 inches. This means that the radius is 10 inches. Find the area:

`A=\pi r^2\\A=\pi (10)^2\\A=100\pi`

Now, find the ratio between them by dividing:

`\frac{\text{Smaller}}{\text{Larger}}=(25\pi)/(100\pi)`

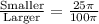
Simplify:

`\frac{\text{Smaller}}{\text{Larger}}=(1)/(4)`

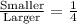
1/4 is the same as 1:4

So, our answer is C :)