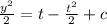Answer:
A) In y = - [ x-In (x+1) ] + c
B)
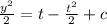
Explanation:
A) tydt + ( t + 1 ) dy = 0
dy/y = - (
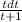 ) we have to integrate both sides of the equation
) we have to integrate both sides of the equation
In y = - [ x- In (x +1) ] + c
B) y dy/dt + t = 1
we can express the equation as :
y dy = ( 1 - t ) dt
when we integrate the equation we have