Answer:
For F=GMm/r^2
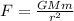
a.
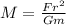
b.
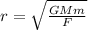
M=kxa^3/p^2
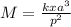
a.
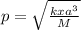
b.
![a = \sqrt[3]{(Mp^(2) )/(kx)}](https://img.qammunity.org/2021/formulas/mathematics/college/mye8jrun3vervoontfl81a00dl917fvi8q.png)
Explanation:
To solve for the unknown quantity, we will make the unknown quantity the subject of the given equation.
For F=GMm/r^2
a. M =
F=GMm/r^2
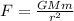
The first thing to do is cross multiply, so that the equation gives
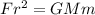
Now, divide both sides of the equation by
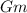 , we then get
, we then get
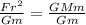
Then,
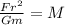
Hence,
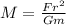
b. r =
F=GMm/r^2
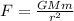
Likewise, we will first cross multiply, we then get
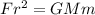
Now, divide both sides by
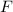 , so that the equation becomes
, so that the equation becomes
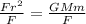
∴
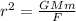
Then,
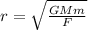
For M=kxa^3/p^2
a. P =
M=kxa^3/p^2
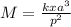
The first thing to do is cross multiply, so that the equation becomes
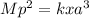
Now, divide both sides by M, we then get
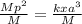
∴
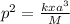
Then,
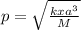
b. a =
M=kxa^3/p^2
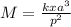
Also, we will first cross multiply to get
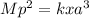
Then, divide both sides of the equation by
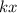 to get
to get
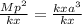
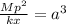
∴
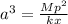
Then,
![a = \sqrt[3]{(Mp^(2) )/(kx)}](https://img.qammunity.org/2021/formulas/mathematics/college/mye8jrun3vervoontfl81a00dl917fvi8q.png)